Optimise Adjacency Matrix Using Bitwise Operations in Tideman Algorithm
Table of Contents
This article will first introduce the background of the Tideman algorithm to enable readers who are not yet familiar with this method to build a comprehensive understanding of the context. Subsequently, it will demonstrate all the main functions of this algorithm. If you are already comfortable with the prerequisite concepts of Tideman, please feel free to jump to the core discussion part directly.
All the code is shared on Github, please feel free to try it out:
Tideman election simulation algorithms using adjacency list, adjacency matrix, and bitwise operations.
1. Background of the Tideman Electoral System #
1.1. Definition #
The Tideman (aka. Ranked pairs) algorithm is an electoral system developed in 1987 by Nicolaus Tideman that selects a single winner using votes that express preferences 12. It is a ranked-choice voting system where voters can vote for more than one candidate in order of preference. A “Condorcet winner”, the person who would have won any head-to-head matchup against another candidate, will be elected from a sorted list of winners in such a system.
1.2. Procedure #
The Tideman voting method operates as follows:
- Tally: Document the winner of each pair of candidates and the margin.
- Sort: Rank each pair, by strength of victory (margin) from largest first to smallest last.
- Lock: Starting with the strongest pair, go through the sorted pairs, and “lock” the pairs that do not create a cycle with the existing locked-in pairs.
- Find: The winner in such a voting system is defined as a person who never appears as a loser in each head-to-head matchup.
1.3. Visualisation #
To enhance clarity, consider this straightforward example for a more comprehensive comprehension.
Tally: Suppose that there are 3 candidates {a, b, c} and 10 voters, such that the votes are tallied as shown in Table 1.
Table 1. Table of Ballots
| a | b | c | |
|---|---|---|---|
| a | 0 | 2 | 6 |
| b | 8 | 0 | 1 |
| c | 4 | 9 | 0 |
Sort: The pairs are then sorted in decreasing order by strength of victory.
Table 2. Sorted Pairs
| winner | loser | strength | |
|---|---|---|---|
| 1 | c | b | 9 |
| 2 | b | a | 8 |
| 3 | a | c | 6 |
Lock: In this step, the Tideman algorithm locks the pairs from the strongest strength and avoids creating cycles. To represent this, we can create a matrix with all the initial values set as “0”, and then use “1” to represent “locked” pairs.
Table 3. Locked Pairs
| a | b | c | |
|---|---|---|---|
| a | 0 | 0 | 0 |
| b | 1 | 0 | 0 |
| c | 0 | 1 | 0 |
Candidate graph
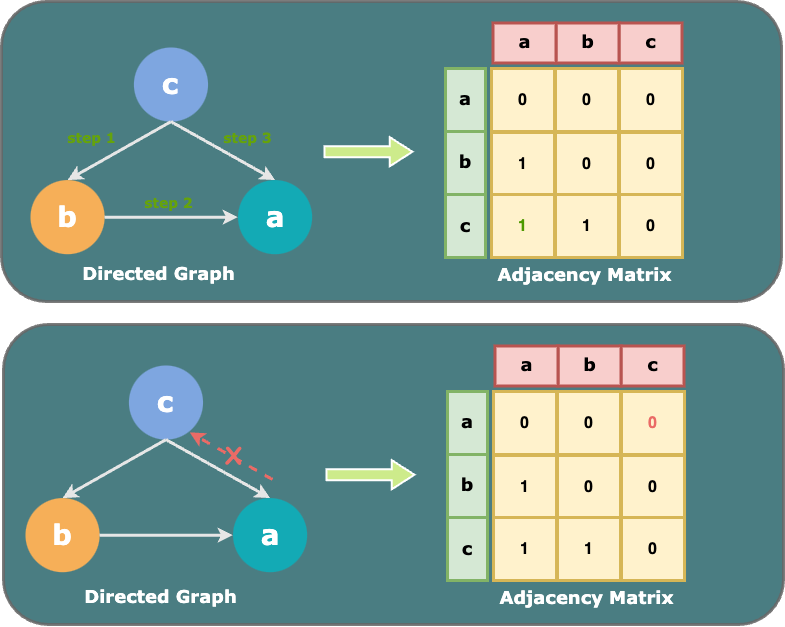
The aforementioned procedure can be illustrated through graphs containing nodes and arrows representing edges. In particular, a node is a candidate, and an edge from candidate a to candidate b indicates that candidate a wins against candidate b in a head-to-head matchup. The matchup edges are “locked” to the graph one at a time, based on the sorted order without creating a cycle. If a cycle is anticipated, the corresponding pair will be omitted.
The graph representing the above process is depicted in Figure 1. According to the Tideman method, the winner of the election is the candidate who never appears as a “loser”; consequently, s/he should be the “source” of the graph with no arrows pointing towards him/her. Therefore, candidate c is considered the winner.
Figure 1. Directed Graph

2. Build the Tideman Electoral System in C #
The crucial steps in the Tideman method include 6 functions: vote, record_preferences,add_pairs, sort_pairs, lock_pairs, and print_winner.
2.1. Record Votes #
The vote function collects ballots from voters and ensures their validity by verifying if the names appear in the candidate list. Afterwards, it proceeds to record the votes.
Following the voting process, the record_preference function generates pairs of winners and losers, counting the occurrences of each pair in the preference array. For example, preference[i][j] = 3 indicates that there are 3 voters that prefer candidate i over candidate j.
bool vote(int rank, string name, int ranks[])
{
for (int i = 0; i < candidate_count; i++)
{
if (strcmp(name, candidates[i]) == 0)
{
ranks[rank] = i;
return true;
}
}
return false;
}
void record_preferences(int ranks[])
{
for (int i = 0; i < candidate_count; i++)
{
for (int j = i + 1; j < candidate_count; j++)
{
preferences[ranks[i]][ranks[j]]++;
}
}
return;
}
2.2. Add Pairs #
The add_pairs function will add all pairs with more votes which means one candidate is preferred over the other among all voters.
For example, if preferences[m][n] = 3 and preferences[n][m] = 2 means more voters prefer m over n, so the pair m -> n will be added to the pairs by assigning m as .winner and n as .loser. If the candidates are tied, they will not be added to the array.
void add_pairs(void)
{
int i = 0;
pair_count = 0;
for (int m = 0; m < candidate_count; m++)
{
for (int n = 0; n < candidate_count; n++)
{
if (preferences[m][n] > preferences[n][m])
{
pairs[i].winner = m;
pairs[i].loser = n;
pair_count++;
i++;
}
}
}
}
2.3. Sort Pairs #
The sort_pairs function sorts the pairs of candidates in pairs in decreasing order based on the strength of victory.
void sort_pairs(void)
{
for (int i = 0; i < pair_count - 1; i++)
{
for (int j = 0; j <= i - 1; j++)
{
if ((preferences[pairs[j].winner][pairs[j].loser]) < (preferences[pairs[j + 1].winner][pairs[j + 1].loser]))
{
pair temp = pairs[j];
pairs[j] = pairs[j + i];
pairs[j + 1] = temp;
}
}
}
return;
}
2.4. Lock Pairs #
The lock_pairs function creates the locked graph by adding all pairs in decreasing order of victory strength while ensuring that each edge does not create a cycle. In this section, three methods are discussed for implementing the lock_pairs function.
This is the most fun part of this algorithm! After exploring together with Juju, we managed to use the bitwise operation method to avoid numerous embedded loops and successfully locked pairs without creating a cycle and find the winner with 10 lines of code in total and achieved O(n) and Ω(1), while also optimising memory usage by \((\frac{n-4}{n})\) comparing to the adjacency matrix method.
2.4.1. Adjacency List Method #
An adjacency list is a data structure used to represent a finite graph. Each list within an adjacency list describes the set of neighbours of a particular vertex in the graph 3.
In the context of Tideman, new pairs are locked in the order of sorted rankings, while ensuring that the newly locked-in pairs do not create a cycle. Transitioning to the concept of the adjacency list, to prevent the creation of cycles with newly added pairs, the following steps should be taken:
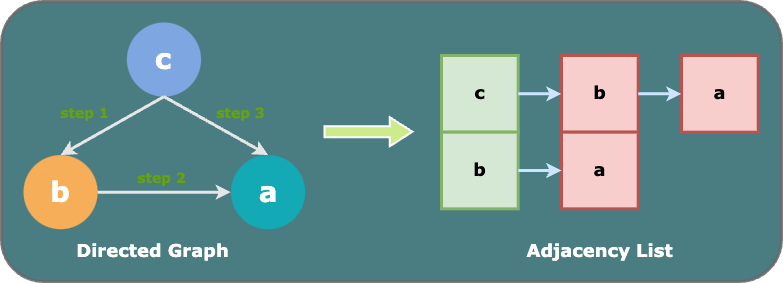
- Link all existing pairs. For instance, if we have pairs {c, b} and {b, a}, we should also link {c, a}. Therefore, Figure 1. can be described by the set of adjacency lists:
{c -> [b, a], b -> [a], a -> []}as shown in Figure 2.
Figure 2. Adjacency List
- Verify if the reverse pair of the new pair already exists. For example, when considering a new pair {a, c}, before locking it, we need to check if {c, a} already exists. If so, it would create a cycle, and the pair {c, a} should be skipped.
Figure 3. Skip Pair to Avoid Creating Cycle

The skeleton of implementing the Tideman algorithm using the adjacency list concept can be summarised in the following steps:
- Create a new empty list
NEWto document all the connections within locked pairs. - Iterate through all the pairs in
pairs:- Check if the new pair will create a cycle with existing connections in
NEW. If not:- Lock the new pair in
lockedand add this pair inNEW. - For each newly added pair, update all the connections in
NEW. To build the connection, simply check if the winner of the new pair ever appeared as the loser in the previous pair, and update the new connections by adding them to the listNEW.
- Lock the new pair in
- Check if the new pair will create a cycle with existing connections in
2.4.2. Adjacency Matrix Method #
The adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix are boolean variables indicating whether pairs of vertices are adjacent in the graph 4. This concise representation allows the adjacency matrix to portray the graph straightforwardly. However, for a sparse graph, an adjacency matrix may require more space compared to an adjacency list since it also allocates space to nonexistent edges.
The concept of building the Tideman algorithm using the adjacency matrix is similar to that of the adjacency list: lock every new pair that will not create a cycle in locked, and then connect all the links for the newly added pair in an adjacency matrix.
Figure 4. Adjacency Matrix
The skeleton of implementing the Tideman algorithm using the adjacency list concept can be summarised in the following steps:
- Create a new empty matrix
NEWto document all the connections within locked pairs. - Iterate through all the pairs in
pairs:- Check if the new pair will create a cycle with existing connections in
NEWby checking if the reverse pair istruein the matrix. If not:- Lock the new pair in
lockedand add this pair inNEW. - For each newly added pair, update all the connections in
NEW. To build the connection, simply iterate all raws and useLogical ORto accept all thetrues fromNEW[j][winner](j that wins over the winner) toNEW[loser](given thatwinner -> loserandj -> winner, we can conclude thatwinner -> loser).
- Lock the new pair in
- Check if the new pair will create a cycle with existing connections in
void lock_pairs(void)
{
bool NEW[MAX][MAX] = {{}};
for (int i = 0; i < pair_count; i++)
{
if (!NEW[pairs[i].loser][pairs[i].winner])
{
locked[pairs[i].winner][pairs[i].loser] = true;
NEW[pairs[i].winner][pairs[i].loser] = true;
for (int j = 0; j < candidate_count; j++)
{
NEW[j][pairs[i].loser] |= NEW[j][pairs[i].winner];
}
}
}
}
2.4.3. Bitwise Operation Method #
Although the adjacency matrix is very straightforward, a concern arises when applying it to a graph with sparse connections, resulting in a matrix predominantly filled with 0 and a scarcity of 1. To optimise memory usage and reduce the average running time that the algorithm takes to find the winners, bitwise operations are incorporated in this section.
A bitwise operation operates on a bit string, a bit array or a binary numeral (considered as a bit string) at the level of its individual bits 5. Bitwise operations commonly use less power because of the reduced use of resources 6. Here is the list of all the bitwise operators with examples.
&Bitwise AND: Conduct AND on every bit of two numbers.int result = 5 & 3; // 101 & 011 -> 001|Bitwise OR: Conduct OR on every bit of two numbers.int result = 5 | 3; // 101 & 011 -> 111^Bitwise XOR: Take 2 numbers, and set different bits as 1, same set as 0.int result = 5 ^ 3; // 101 & 011 -> 110~Bitwise NOT: Inverts all bits in a number.int result = ~5; // 0000 0000 0000 0000 0000 0000 0000 0101 -> 1111 1111 1111 1111 1111 1111 1111 1010<<Left shift: Shifts the bits of the first operand to the left by the number of positions specified by the second operand.int result = 5 << 2; // 101 << 10100>>Right shift: Shifts the bits of the first operand to the right by the number of positions specified by the second operand.int result = 20 >> 3; // 10100 >> 10
In the context of tideman, pair {pair[i].winner,pair[i].loser} will represent as winnerth bit in the binary format of NEW[pair[i].loser]. We can use 1 << n to represent nth bit of NEW[i] (e.g.: 1 << 2 = 100, which sets the 2th bit to 1). We can use & to check if nth bit is 0 or 1 and use | to set nth bit to 1.
Figure 5. Bitwise Operations with Examples

The skeleton of implementing the Tideman algorithm incorporating the bitwise operations can be summarised in the following steps:
- Create a new empty array
NEWwith the size of the maximum candidate count and initialise all elements of the array to0. - Iterate through all the pairs in
pairs:- Use
&to check if the new pair will create a cycle with existing connections inNEWby verifying if the loserth bit of the winnerth item inNEWalready exists. If not, lock the new pair inlockedand add this pair and all connections inNEWusing|=.
- Use
void lock_pairs(void)
{
int NEW[MAX] = {};
for (int i = 0; i < pair_count; i++)
{
if (!(NEW[pairs[i].winner] & (1 << pairs[i].loser)))
{
locked[pairs[i].winner][pairs[i].loser] = true;
NEW[pairs[i].loser] |= ((1 << pairs[i].winner) | NEW[pairs[i].winner]);
}
}
}
2.5. Find the Winner #
2.5.1. Find the Winner with Adjacency List and Adjacency Matrix #
The print_winner function will print out the names of the candidates who are the winners under Tideman algorithm. The winners should be the “source” of the graph meaning that no arrows point to them.
For the adjacency list and adjacency matrix method, the print_winner checks every loser column in locked, and breaks if meets any true (which means this candidate was a loser in a pair).
void print_winner(void)
{
for (int j = 0; j < candidate_count; j++)
{
bool is_winner = true;
for (int i = 0; i < candidate_count; i++)
{
if (locked[i][j])
{
is_winner = false;
break;
}
}
if (is_winner)
{
printf("%s\n", candidates[j]);
}
}
}
2.5.1. Find the Winner Using Bitwise Operation #
For the bitwise operation method, print_winner just needs to simply find all the 0s in the array NEW.
void print_winner(void)
{
for (int k = 0; k < candidate_count; k++)
{
if (NEW[k] == 0)
{
printf("%s\n", candidates[k]);
}
}
}
Combining the lock_pairs and print_winner together, here is all we need using the bitwise operations to find the winners.
void find_winners(void)
{
int NEW[MAX] = {};
for (int i = 0; i < pair_count; i++)
{
if (!(NEW[pairs[i].winner] & (1 << pairs[i].loser)))
{
locked[pairs[i].winner][pairs[i].loser] = true;
NEW[pairs[i].loser] |= ((1 << pairs[i].winner) | NEW[pairs[i].winner]);
}
}
for (int k = 0; k < candidate_count; k++)
{
if (NEW[k] == 0)
{
printf("%s\n", candidates[k]);
}
}
}
This article discussed how to apply bitwise operation in Tideman voting algorithm. As one of many ways of implementing this algorithm, I hope it is straightforward, entertaining, and helpful. Also, a big thanks to Juju for making the exploration journey so much fun, and CS50 staff for bringing us such an amazing exercise!
Tideman, T. N. (1987). Independence of clones as a criterion for voting rules. Social Choice and Welfare, 4, 185-206. ↩︎
Schulze, M. (2011). A new monotonic, clone-independent, reversal symmetric, and condorcet-consistent single-winner election method. Social choice and Welfare, 36, 267-303. ↩︎
“CMicrotek Low-power Design Blog”. CMicrotek. Retrieved 2015-08-12. ↩︎

